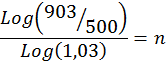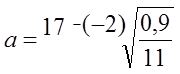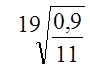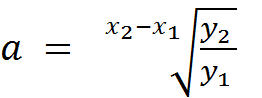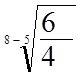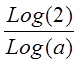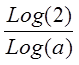Dette hæfte er en del af et interaktivt læresystem i matematik hf, og beregnet til at blive brugt på en pc koblet på Internettet. Herved bliver det muligt at benytte diverse links til E-opgaver, interaktive opgaver og til videoer. Sideløbende hermed kan det være praktisk at benytte en papirudgave, som kan printes direkte fra http://mahf.dk/del1/start.pdf , som er

i et printvenligt PDF-format. De fleste links er inaktive i den printvenlige udgave.

Videoerne bør ses i brudstykker på kun nogle få minutter af gangen.

Besvarelser af E-opgaver sendes automatisk via Internettet til læreren.

Med denne matematik-pakke følger endvidere et elektronisk afleveringsark, RegneRobot med matematik-editor og CAS , hvor elever/kursister kan besvare opgaver og også her automatisk få sendt opgavebesvarelserne til læreren.

RegneRobot indeholder en række faciliteter, der gør det lettere at besvare opgaver.

Indholdsfortegnelsen kan benyttes som links.

Uanset hvor man er i dokumentet, kan man komme til indholdsfortegnelsen ved at taste Ctrl+Home , PageDown , PageDown.

Søgning på bestemte ord (svarende til stikordsregister) foretages ved at taste Ctrl+f

I denne version, Matematik C interaktivt for hf, version 8.6 er i lektion 12 tilføjet en omtale af graf-programmet GraphSketch. Desuden er der sket en lille ændring i del 2 (blåt hæfte), lektion 18c, ”Eksempel på eksamensspørgsmål”.
Facitlisten i de tidligere versioner er fjernet i denne og i version 8.5, men erstattet af links til en facitliste. Ellers er denne version næsten magen til de tidligere versioner.

Denne undervisningspakke er under stadig udvikling. Forslag og eventuelle rettelser til denne pakke modtages med tak på lyngbydata.dk/rettelser

Matematik-pakken kan bestilles via lyngbydata.dk/pakke /Peter Sørensen

Lektion 1: Brøk

Udfør følgende 5 punkter

1) læs:

Motivation til brøk-regning og til ligninger

Opgave:

En taxa koster 25 kr i startgebyr og 12 kr pr km.

En køretur kom til at koste 115 kr

Hvor mange km blev kørt

Besvarelse:

(Måske forstår du ikke besvarelsen, men bliver så til gengæld motiveret til at lære om brøker og om ligninger, som vi senere skal i gang med)

Lad x betegne antal km.

Der gælder

12x + 25 = 115

12x = 115 - 25

12x = 90

x = ⁹⁰/₁₂
x = ¹⁵/₂

x = 7¹/₂

DVS: Der blev kørt 7,50 km

2) Se video. Link: Brøkregning

3) Løs interaktivt. Link: Brøkstykker Se regler side 46 i DEL 2

Hvis det kniber med de 4 regningsarter så klik her: Opgaver i de 4 regningsarter og Den lille tabel

4) Løs E-opgaver. Link: E-opgaver_01_broek.htm
Du afleverer elektronisk, når du klikker i Aflever .

5) Løs fra 2006-opgavehæftet 1.006

Klik i opgavenummeret og se en demo-video.

Også i RegneRobot afleveres elektronisk ved at klikke i Aflever

Link til RegneRobot & opgavehæfte

Her er et eksempel på en skabelon til besvarelse af 1.006

Jeg skal beregne, hvor mange sms´er, der er sendt. Hver sms koster 0,20 kr og hvert min. samtale 0,70 kr En regning var på 486 kr og der var 630 min samtale.
Samtalerne har kostet	630*0,70 kr	=
Sms´erne har kostet		=
Konklusion: Så mange sms´er blev der sendt:		=

Lektion 2: Ligninger

Udfør følgende 5 punkter

1) Læs

Du står i regnskoven, og en oversvømmelse er på vej. Det er begyndt at regne vedvarende. Lige nu er der 9 cm vand, og vandstanden stiger ²/₃ cm hvert minut.

Du går nu i gang med at bygge en tømmerflåde; men du har travlt. Når vandstanden kommer op på 75 cm er det umuligt at arbejde, så du skal være færdig inden.

Du har nu x minutter til at bygge tømmerflåden.

Vi vil finde den ubekendte størrelse x.

Der må gælde:

9 + ²/₃ · x = 75

Det kalder vi en ligning.

At løse en ligning vil sige, at finde det eller de tal, der indsat i stedet for den ubekendte får lighedstegnet til at passe.

Vi laver nogle omskrivninger af ligningen til nogle mere enkle ligninger, der har samme løsning. Det kaldes lovlige omskrivninger.

Først laver vi en omskrivning, så vi undgår brøk.

Det gør vi ved at gøre både venstresiden og højresiden 3 gange så stor.

27 + 2x = 225

Bemærk 2x er det samme som 2·x
og bemærk, alle led er ganget med 3.

Næste trin er at isolere 2x. Det gør vi ved at fjerne 27 på begge sider af lighedstegnet.

2x = 225 – 27

Man kan også sige, vi flytter 27 over på den
anden side af lighedstegnet og skifter fortegn.

Vi kan nu udregne højresiden

2x = 198

Ved at dividere med 2 på begge sider af lighedstegnet er x isoleret og ligningen løst.

x = 99

Konklusion: Du har 99 minutter til at bygge tømmerflåden.

Når man løser en ligning ved lovlige omskrivninger, kan man sætte denne dobbeltpil ó mellem ligningerne. Dobbeltpil mellem 2 lignigner betyder, de har samme løsning, fx:

9 + ²/₃ · x = 75 ó 27 + 2x = 225 ó 2x = 225 - 27ó 2x = 98 ó x = 99

Ofte undlader man dobbeltpil og går blot på ny linje ved hver omskrivning.

Her bringes en oversigt over lovlige omskrivninger ved løsning af ligninger.

Lovlige omskrivninger ved løsning af ligninger

Regler:

Eksempler på
anvendelse af reglerne:

Man kan flytte et led over på den anden side af lighedstegnene, hvis man samtidig ændrer fortegn.

27 + 2x = 225

ó 2x = 225 - 27

Almindelige udregninger

2x = 225 - 27

ó 2x = 198

Man må dividere eller gange med samme tal på begge sider, dog ikke med nul.

9 + ²/₃ · x = 75

ó 27 + 2x = 225

2x = 198

ó x = 99

Godt råd

Flyt x til den side, hvor der er flest og hold tallene på den anden side.
Bemærk -2 er større end -5 .

Eks. 7 - 5x = -2x + 1 ó 7 - 1 = -2x + 5x ó 6 = 3x ó 2 = x

Pas på

Når man ganger eller dividerer på begge sider, skal det gøres ved samtlige led.

Led adskilles fra hinanden af plus eller minus. I udtrykket 5·3+7 er 2 led: 5·3 og 7.

Fx ½x + 1 = 4 ó x + 2 = 8 ó x = 8 – 2 ó x = 6

Eksempler

Eks 1

5 = 2x + 3

5-3 = 2x

2 = 2x

1 = x

Eks 2

²/₃x+ 5 = x – ²/₅

2x + 15 = 3x - ⁶/₅

10 x +75 = 15x – 6

75 + 6 = 15x – 10x

81 = 5x

16,2 = x

Eks 3

2x + 3 = 2x

2x – 2x = -3

0 = -3

Det er aldrig sandt og ligningen har ingen løsning

Eks 4

1+2x+2 = 2x+3

2x – 2x = 3 – 1 – 2

0 = 0

Det er altid sandt
uanset x og alle tal
er løsning

2) Se Video. Link: Ligninger

3) Gør øvelse med følgende 4 opgaver:

1. 2x + 3 = x+ 5

2. 3x – 7 = 5x – 11

3. ½b +3 = 6 – b Bemærk: Den ubekendte behøver ikke at være x.

4. 1/3 x - 11 = 2x - 77

Facits:

1. x=2

2. x=2

3. b=2

4. x=39,6

3) Løs ligninger interaktivt. Link: Interaktive ligninger

4) Løs E-opgaver. Link: E-opgaver_02_ligninger.htm

5) Løs fra 2006-opgavehæftet 1.003

Klik i opgavenummeret og se en demo-video.

Også i RegneRobot afleveres elektronisk ved at klikke i Aflever .

Link til RegneRobot & opgavehæfte

Eksempel på skabelon til løsning af 1.003

A = 4 · π · r² (π er lig ca. 3,14 og indgår i formlen for arealet af en cirkel). I RegneRobot skrives π således: pi()

Ved at indsætte 1000 i stedet for A fås:

1000 = 4 · π · r² ó 1000/(4·π) = r²

ó r² =

ó r =

Konklusion: Radius er cm

Link: Indholdsfortegnelse

Lektion 3: Eksponent og rod

Udfør følgende 5 punkter

1) Se video. Link: Eksponenter

2) Læs:

Eksponent

5·5·5 skrives forkortet 5³ og udtales: ”Fem i tredje” eller ”Fem i tredje potens”.

3-tallet foroven kaldes eksponenten.

5³ kan også skrives 5^3.

Vi arbejder også med eksponenter, der ikke er hele positive tal, fx 5^2,5

Vi vil dog ikke her komme ind på hvordan disse eksponenter defineres.

Der arbejdes også med negative eksponenter. Betydningen fremgår af følgende eksempel:

5^-3 =

₁

Regler for regning med eksponenter

Disse regler vil ligeledes blive illustreret med eksempler:

5³ · 5⁴ = 5³⁺⁴ idet 5·5·5 · 5·5·5·5 = 5³⁺⁴

5⁷

5³

= 5^7-3 idet

5·5·5·5·5·5·5

5·5·5

= 5⁴

(5·7)³ = 5³· 7³ idet 5·7 · 5·7 · 5·7 = 5·5·5 · 7·7·7

(5³)⁴ 5^3·4 = 5¹² idet (5³)⁴ = 5·5·5 · 5·5·5 · 5·5·5 · 5·5·5

5¹ = 5

5⁰ = 1

8³: 5³

= (

)³ idet

(

)³ =

8·8·8

5·5·5

Se regler for eksponenter i formelsamlingen

Rod

Hvis man ønsker at arbejde med et tal, som ganget med sig selv 3 gange giver 125, kan det skrives:

^. ____
√ 125

Der gælder

^. ____
√ 125

= 5 , fordi 5³ = 125

^. ____
√ 125

udtales: ”Den 3. rod af 125” og ikke: ”~~Den 3. kvadratrod af 125~~”

Bemærk 3

^. ____
√ 125 = 125^(1/3) = 125^(1/3)

Denne omskrivning er praktisk på lommeregner og nødvendig i regneark.

Bemærk endvidere:

^. __
√ 9

= 9^0,5 = 9^(1/5) = 3

^. __
√ 9

udtales: ”Kvadratroden af 9” eller: ”Den anden rod af 9”

Se også formelsamlingen side 54 i DEL 2 (blåt hæfte).

3) Løs denne øvelse: Link: Eksponenter

4) Løs E-opgaver: Link: E-opgaver_03_eksponent_og_rod.htm

5) Løs fra 2006-opgavehæftet 1.008

Klik i opgavenummeret og se en demo-video.

Også i RegneRobot afleveres elektronisk ved at klikke i Aflever .

Link til RegneRobot & opgavehæfte

Lektion 4: Regnearternes hierarki og parentes mm.

Udfør følgende 7 punkter

1) læs:

Regnearternes hierarki

Lad os beregne 5+2·3. Resultatet er 11. Bemærk at vi først udregner 2·3. Vi siger gange går forud for plus og taler om regnearternes hierarki.

Den hierarkiske orden er som følger:

1. Potensopløftning og rod

2. Gange og division

3. Plus og minus

Eksempel: 5 -

__________ ____________
√ 9

= 5 -

= 5 - 2 = 3

De størrelser i et regneudtryk, som adskilles af plus eller minus kaldes led.

De størrelser i et regneudtryk, som adskilles af gange kaldes faktorer.

Parenteser

Ved hjælp af parenteser kan regnearternes hierarki brydes, idet parenteser skal udregnes først.

Fx (3+5)·10 = 8·10 = 80

Hvis der er parentes inden i en parentes, skal den inderste udregnes før den yderste.

Fx (4⁽²⁺¹⁾+ 5)·10 = (4³+ 5)·10 = (64 + 5)·10 = 69·10 = 690

Opgave:
Jensen har et hus, som er 7 meter bredt og 8 meter langt .

Han vil gerne forlænge huset så meget som muligt; men kommunen vil kun tillade et hus på højst 100 m².

Hvor mange meter kan Jensen forlænge sit hus, når bredden fortsat skal være 7 meter?

Denne opgave kan løses ved at opstille en ligning; men vi får også brug for parentes.

Besvarelse af opgaven:

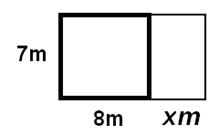Forlængelsen i meter betegnes x

Husets nye længde i meter bliver 8 + x

Målt i m² er det nye areal: 100 ;

men arealet er også 7 · (8 + x)

Her har vi sat parentes uden om 8 + x.

Det betyder, vi i princippet skal udregne 8 + x inden vi ganger med 7, hvilket er umuligt, da vi ikke kender x

Imidlertid kan vi bruge en regel, som siger, at 7 · (8 + x) = 7 · 8 + 7 · x

Denne regel kan udtrykkes med en formel: k · (a+b) = ka + kb

hvor k svarer til 7, a svarer til 8 og b svarer til x.

Vi kan derfor opstille følgende ligning:

7 · (8 + x) = 100

7 · 8 + 7 · x = 100

56 + 7x = 100

7x = 100 - 56

7x = 44

x = 6²/₇

Dvs. Jensen kan forlænge sit hus 6²/₇ m

Den regel vi brugte, kan udtrykkes ved:

Man ganger med en parentes ved at gange med hvert led i parentesen.

Vi vil ikke bevise formlen; men formentlig kender du den udmærket og bruger den tit uden egentlig at vide det, fx hvis du i hovedet skal udregne 7 · 12.

Idet 12 = 10+2, vil du formentlig sige: 7·10 + 7·2 = 70 + 14 = 84.

Regnestykket kan skrives
7 · 12 = 7 · (10 + 2) = 7 · 10 + 7 · 2 = 70 + 12 = 84

Hvilket er i overensstemmelse med formlen.

Ved parentes gange parentes kan man generelt benytte følgende regel, som vi heller ikke vil bevise:

Man ganger 2 parenteser med hinanden ved at gange hvert led i

den ene med hvert led i den anden.

Fx: (x+3) (x+4) = x² + 4x + 3x + 12 = x² + 7x + 12

Se regler for parenteser i formelsamlingen

Fortegn ved multiplikation af 2 faktorer

Hvis faktorerne har forskelligt fortegn er resultatet negativt.

Eksempel: 3·(-5) = -15

Hvis faktorerne har samme fortegn er resultatet positivt.

Eksempel: (-3)·(-5) = 15

Fortegn ved division

Hvis tæller og nævner har forskelligt fortegn er resultatet negativt.

Eksempel: ²⁰/_-5= -4

Hvis tæller og nævner har samme fortegn er resultatet positivt. Eksempel: ^-²⁰/_-5 = 4

2) Se video. Link: parentes og regler side 47 i DEL 2

3) Løs interaktivt. Link: PARENTES

4) Løs. Link: Øvelse

5) Gør øvelse med følgende opgaver:

Facits:

1. 8(½x – 5) = x – 60 x = -6²/₃

2. 7(2x + 5) = 3(x – 17) x = -7⁹/₁₁

3. ²/₅(x – 12) = ½(3x + 5) x = -6⁷/₁₁

4. 4(¹/₃x + 2) = 20 x = 9

5. 7(3x – 5) = 3(x-7) x = ⁷/₉

6. 2(x+8) = ½(5x – 17) x = 49

7. 2(x+(2·3+2)) = ½(5x – 17) x = 49

6) Løs E-opgaver Link: E-opgaver_04_parentes

7) Løs fra 2006-opgavehæftet 2.013

Benyt RegneRobot med link til opgavehæftet. Klik i opgavenummeret og se en demo-video. Også i RegneRobot afleveres elektronisk ved at klikke i Aflever

Link til RegneRobot & opgavehæfte

Lektion 5: Procent og rente

Udfør følgende 5 punkter

1) Læs:

Procent spiller en stadig større rolle i samfundsdebatten. Flere og flere henviser til procenter når de udtaler sig om dette eller hint.

Procent betyder pr 100.

Fx 2% betyder 2 pr 100 eller ²/₁₀₀= 0,02

Man lægger 2 % til et tal ved at gange med 1,02 eller (1+2%)

Fx lægger man 2% til 300 ved at sige 300·1,02 = 306

Man kan også regne sig frem til 306 ved at sige 300 + 2% af 300 = 300 + 6 = 306; men det er mere besværligt, især ved rentes rente, som vi skal se på om lidt. .

Man trækker 10% fra ved at gange med (0,90 ) eller (1-10%).

Man kan sige der her er tale om at lægge -10% til.

Generelt gælder:

Man lægger p% til ved at gange med (1+p%) eller med (1+r) , hvor r = p%

(1+r) kaldes fremskrivningsfaktoren og

r kaldes rentefoden, hvis det handler om renter, ellers vækstraten.

Hvis vi får 2% i rente pr termin, siger vi, at rentefoden er 2% eller 0,02

Renteformlen

Hvis et beløb forrentes gennem flere terminer, vil man også få rente af renterne. Det kaldes Rentes rente.

Lad os betragte 300 kr som forrentes med 2% pr år i flere år:

Efter 0 år er beløbet 300 kr

Efter 1 år er beløbet 300·1,02 kr

Efter 2 år er beløbet 300·1,02·1,02 kr = 300·1,02²

Efter 3 år er beløbet 300·1,02²·1,02 kr = 300·1,02³

Efter 4 år er beløbet 300·1,02⁴

·······

Efter n år er beløbet 300·1,02ⁿ

De 300 kr kaldes begyndelseskapitalen og betegnes K_o
Beløbet efter n rentetilskrivninger kaldes slutkapitalen og betegnes K_n eller blot K.

Generelt gælder renteformlen:

K = K₀ · (1+r)ⁿ

Fx: K₄ = 300·1,02⁴

Den vil vi ikke bevise. Vi nøjes med ovenstående anskueliggørelse.

Bemærk: K₀= K₀ · (1+r)⁰ , idet (1+r)⁰ = 1 og K₁= K₀ · (1+r)¹ = K₀ · (1+r)

Fremskrivningsfaktor

Når man ganger et tal med 1,02, siger vi, at tallet er blevet fremskrevet med 2% og 1,02 kaldes fremskrivningsfaktoren.

Generelt kan man sige, at hvis man har to tal forskellige fra nul, så kan man komme fra det ene tal til det andet ved at gange med en passende faktor.

En sådan faktor kaldes fremskrivningsfaktor.

Lad os betragte to tal 300 og 306.

Der gælder 306 = 300 · 1,02.

Her er 1,02 fremskrivningsfaktoren.

Man siger, 300 er blevet fremskrevet til 306 med fremskrivningsfaktoren 1,02.

Man kan også sige, at 300 er blevet fremskrevet til 306 med 2%

Når man kender de to tal 306 og 300 kan fremskrivningsfaktoren beregnes således: ³⁰⁶/₃₀₀ = 1,02, og derefter kan man konkludere, at ændringen er 2%.

Ved rentesregning kaldes (1+r) for fremskrivningsfaktoren svarende til én rentetilskrivning, dvs. svarende til én termin.
Ofte siges blot fremskrivningsfaktor, og så er det underforstået, at det svarer til én rentetilskrivning.

(1+r)ⁿ er fremskrivningsfaktoren for n terminer.

Eksempel:

Vækstraten er 20%, så fremskrivningsfaktoren for 3 terminer er: 1,20³ = 1,728. Den procentvise ændring for samtlige 3 terminer bliver 72,8%

2) Se video. Link: Procent og rente

3) Løs Øve-opgaver. Link: Beregn slutkapital

4) Løs E-opgaver. Link: E-opgaver_05_pct-rente

5) Løs fra 2006-opgavehæftet 2.014

Benyt RegneRobot med link til opgavehæftet.

Klik i opgavenummeret og se en demo-video.

Link til RegneRobot & opgavehæfte

Lektion 6: Lommeregner , RegneRobot m.m.

Udfør følgende 3 punkter

1) Læs og løs øvelser:

Lommeregnere

På de fleste lommeregnere indtastes eksponenter ved hjælp af ^.

Fx 5⁴ indtastes som regel: 5^4

Ved nogle lommeregnere benyttes tasten x^y eller y^x i stedet for ^

Den største vanskelighed på de fleste lommeregnere er at indtaste rod-udtryk, og det gøres forskelligt fra lommeregner til lommeregner; men ofte er det lettere at omskrive et rod-udtryk til et udtryk med eksponent.

Eksempel: 3

^. ____
√ 125 = 125^(1/3) = 125^(1/3)

og det sidste udtryk er let at indtaste på de fleste lommeregnere. Parentesen er vigtig.

Mellemresultater bør gemmes i lommeregnerens hukommelse. Det giver større nøjagtighed i beregningerne. Lommeregneren husker langt flere decimaler end den viser i vinduet.

Du kan i en opgavebesvarelse fx skrive 0,43… , og det betyder, at tallet er gemt i din lommeregner med langt flere end de viste 2 decimaler.

På de fleste lommeregnere kan du gemme det tal, som vises i vinduet ved at taste STO og derefter vælge et bogstav eller et tal. (STO er en forkortelse af det engelske ord store)

Når du senere skal regne videre på mellemresultatet, skal det ikke indtastes med alle sine decimaler. Man skal som regel blot taste RCL og det bogstav eller det tal, som du valgte, da du gemte mellemresultatet.

RCL er en forkortelse af det engelske ord recall.

Hvis RCL ikke står på selve tasten men oven over, så er det fordi, man skal benytte tastens sekundære betydning. Det gøres på de fleste lommeregnere ved først at taste 2nd.

På nogle lommeregnere kan man benytte bogstaver i regneudtryk.

Hvis du fx har gemt tallet 27 og valgt bogstavet B, da du gemte, kan du taste 3+B og få 30.

Øvelse 0
_a._{Tag lommeregneren frem og find}

^. ____
√ 125

b. Eksperimenter med lommeregnerens hukommelse.

Regneark
Regneark er opbygget af celler, og hver celle udpeges ved et bogstav og et tal.

Bogstavet fortæller hvilken søjle, cellen er i, og tallet, hvilken række.

Man kan skrive tal og almindelig tekst i hver celle. Tekst bør indledes med en apostrof.

Desuden kan man skrive regneudtryk. Regneudtryk skal starte med et lighedstegn.

Antal decimaler kan styres ved at klikke i eller , som du finder i en menu-linje foroven.

Sådan laves beregninger

Øvelse 1

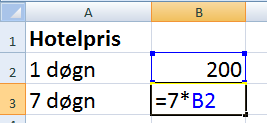
Aktiver regneark og udfyld som nedenfor.
Udfyld celle B3 til sidst. Når du derefter trykker Enter, vil det specificerede regnestykke i celle B3 blive beregnet.

=7*B2 betyder, at 7*200 skal beregnes, fordi der i celle B2 står 200.

Oersigt over regnearter i regneark

	Regneart	Eksempel	Nedenstående udregnes, idet indholdet af B3 er 20
+	Plus	=B3+5	20+5
-	Minus	= B3-5	20-5
*	Gange	= B3*5	20·5
/	Division	=B3/5	²⁰/₅
^	Potensopløftning	=B3^5	20⁵
	Rod	=B3^(1/5)

Bemærk, at der ikke er noget rodtegn i regneark. Man klarer sig med potens.

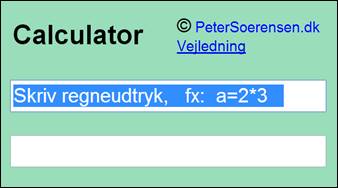
Calculator.dk

er en web-side, der gør det ud for en lomme-regner. Man benytter computerens tastatur.

Når man skriver regnestykket i det første rum og taster Enter, kommer facit i det andet rum.

Hvis man skriver a=2*3, huskes facittet 6 i bogstavet a, og man kan så senere fx skrive 5a og få svaret 30.

Regneudtryk i Calculator.dk

Regneudtryk skrives på næsten samme måde som i almindeligt regneark.
Se nedenstående skema.
Decimalkomma og decimalpunktum kan bruges i flæng. (7,5 = 7.5)

Følgende skrivemåder benyttes i Calculator.dk

Gange	*	fx: 7*3 i stedet for 7·3
Division	/	fx: 1/2 i stedet for ½
Potensopløfting:	^	fx: 5^2 i stedet for 5²
Kvadratrod	Kvrod ^(1/2) ^0,5	fx: Kvrod(9) eller 9^0,5 i stedet for ²√9
n'te rod	nrod ^(1/n)	fx: nrod(3;27) Bemærk semicolon ; eller 27^(1/3) i stedet for ³√27
π	PI()	PI() = π = 3,14…
Almindelig logritme	Log Log10	fx: Log(10)=Log10(10)=1
Naturlig eksp.funktion	eksp exp	fx: eksp(1) = exp(1) = e og eksp(2) = exp(2) = e²
Naturlig logaritme	Ln	fx: Ln(eksp(7)) = 7
Omvendte til Sinus	ArcSin Sin^-1	fx: ArcSin(1/2) = Sin^-1(1/2) = 30°
Omvendte til Cosinus	ArcCos Cos^-1	fx: ArcCos(1/2) = Cos^-1(1/2) = 60°
Omvendte til Tangens	ArcTan Tan^-1	fx: ArcTan(1/2) = Tan^-1(1/2) = 45°

RegneRobot

RegneRobot er en matematik-editor og er beregnet til at hjælpe med at få en pænere opstilling samt automatisk beregning.
RegneRobot er især beregnet til at løse matematikopgaver ved gymnasialt C og B-niveau.
I RegneRobot findes en facilitet Guide & CAS, der hjælper med at løse opgaver.

I RegneRobot skriver du matematik i IT-format, og RegneRobot laver det om til matematik-format og foretager automatisk beregning.

Du skriver fx:

Kvadratet har arealet 25 cm^2

Sidelængden er KvRod(25) cm

Og RegneRobot printer:

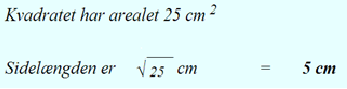
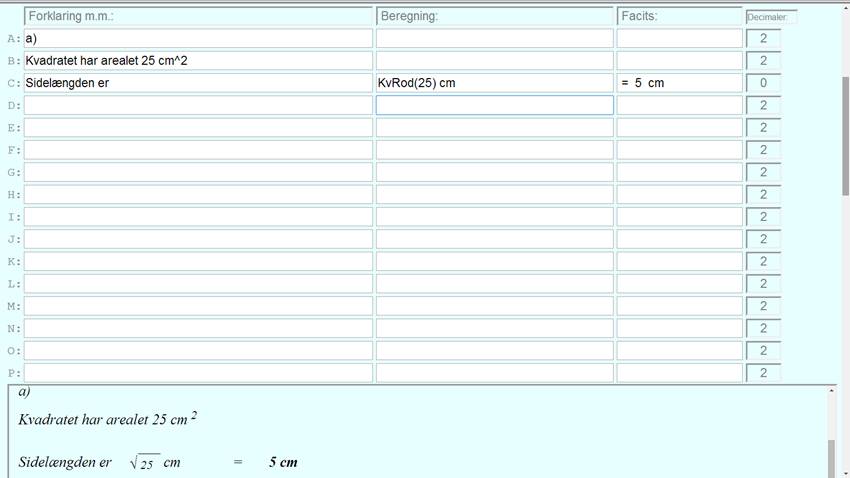
I venstre spalte skriver du, hvad du vil udregne, typisk forklarende tekst eller en svarsætning.
Ved nogle opgaver benyttes kun venstre spalte.
Du kan skrive næsten lige hvad du vil i venstre spalte.

Hvis Du kommer til at slette noget i et felt eller skrive forkert, kan du taste Ctrl+z.

I midterste spalte kan du skrive et regneudtryk og eventuel enhed (benævnelse) (fx 5*1,20 kr) .
Hvis du skriver benævnelse, skal regneudtrykket og benævnelsen være adskilt af et mellemrum.
Der må ikke være mellemrum i selve regneudtrykket.
Hvis Du kommer til at slette noget i et felt eller skrive forkert, kan du taste Ctrl+z.

I kolonnen helt til højre skriver du det antal decimaler, som resultatet (eller mellemresultatet) skal vises med, og facit toner frem med eventuel benævnelse, idet regneudtrykket udregnes automatisk.
Hvis du ikke har anført antal decimaler benyttes enten 2 decimaler eller det antal decimaler, som sidst er indtastet i cellen.

Regneudtryk i RegneRobot
Regneudtryk skrives på næsten samme måde som i almindeligt regneark.
Se nedenstående skema.
Decimalkomma og decimalpunktum kan bruges i flæng. (7,5 = 7.5)
Der må ikke optræde mellemrum i selve regneudtrykket.
Hvis du skriver benævnelse/enhed skal der være mellemrum lige efter regneudtrykket, før benævnelsen/ enheden. Fx: 1,25*8 kr

Du må ikke skrive: ~~1,25 kr *8~~ men gerne: (1,25*8) kr

Følgende skrivemåder benyttes i RegneRobot (Næsten som i Calculator.dk)

Sæt lig med	= := =:	fx: a=7+3 eller a:=7+3
Gange	* ·	fx: 7*3 eller 7·3
Division	/	fx: 1/2 i stedet for ½
Potensopløfting:	^	fx: 5^2 i stedet for 5²
Sænket skrift:	_	fx: x_3 i stedet for x₃
Kvadratrod	KvRod Sqrt ^(1/2) ^0,5	fx: KvRod(9), Sqrt(9) eller 9^0,5 i stedet for
n'te rod	nRod ^(1/n)	fx: nRod(3;27) Bemærk semicolon ; eller 27^(1/3) i stedet for ³√27
π	pi()	PI() = π = 3,14… Ved matematikformat konverteres pi() til symbolet π.
Almindelig logritme	Log Log10	fx: Log(10)=Log10(10)=1
Naturlig eksp.funktion	eksp exp	fx: eksp(1) = exp(1) = e og eksp(2) = exp(2) = e^2
Naturlig logaritme	Ln	fx: Ln(eksp(7)) = 7
Omvendte til Sinus ( Sin^-1 )	ArcSin Sin^-1	fx: ArcSin(1/2) = Sin^-1(1/2) = 30°
Omvendte til Cosinus ( Cos^-1 )	ArcCos Cos^-1	fx: ArcCos(1/2) = Cos^-1(1/2) = 60°
Omvendte til Tangens ( Tan^-1 )	ArcTan Tan^-1	fx: fx: ArcTan(1) = Tan^-1(1) = 45°

2) Se videoer. Link: Demo af RegneRobot

3) Løs E-opgaver. Link: E-opgaver_06_lommeregnerOgRegneark.htm

Der er ingen opgaver fra 2006-opgavehæftet i denne lektion
Lektion 7:
Procent og rente fortsat, gennemsnitlig %-vis ændring

Udfør følgende 7 punkter

1) Læs

I lektion 5 så vi renteformlen:

K = K₀ · (1+r)ⁿ

Ved hjælp af den kan man udregne slutkapitalen K, når man kender begyndelseskapitalen K₀, rentefoden r og antallet af terminer n.

Nogen gange kender man slutkapitalen, men ikke begyndelseskapitalen og vil gerne beregne den. Andre gange kender man ikke rentefoden og vil gerne vide den. Atter andre gange vil man gerne bestemme antallet af terminer.

Vi skal i denne lektion se på de ting.

Begyndelseskapitalen K₀

Vi vil først finde en formel for K₀

Vi isolerer K₀ i renteformlen ved at dividere med (1+r)ⁿ på begge sider af lighedstegnet og får:

Det kan også skrives:

og hermed har vi en formel for K₀ skrevet på 2 måder.

Hvis et beløb fx vokser med 20% pr år og efter 4 år er blevet til 414,72 kr, kan vi beregne startbeløbet 4 år før således: 414,72·1,20^-4 kr = 200,00 kr

Rentefoden / vækstraten r

Vi bemærker, at vækstrate og rentefod betyder det samme; men vi siger rentefod, hvis det handler om renter.

Vi vil nu se, hvordan man bestemmer r .

Vi forudsætter, at r er konstant, dvs r ændrer sig ikke fra termin til termin.

Når man skal bestemme r , kan det gøres ved først at bestemme fremskrivningsfaktoren og så trække én fra, idet (1+r) – 1 = r

Derefter kan man gange med 100%, hvis man ønsker r i %.

Eksempel 1:

Ole optager et kviklån på 1000 kr til en fast årlig rentefod.

Lånet skal tilbagebetales efter 4 år.

Ole får et sjok.

Det viser sig, at Ole skal tilbagebetale lånet med 16000 kr efter kun 4 år.

Hvad har den årlige rentefod været?

Vi indsætter de størrelser, vi kender i renteformlen	K = K₀ · (1+r)ⁿ
og får en ligning med r som ubekendt:	16000 = 1000· (1+r)⁴
Vi dividerer ligningen med 1000	16 = (1+r)⁴
Vi tager den fjerde rod på begge sider (Man kan ikke tage den fjerde rod af negative tal; men her er tale om positive tal. Ligningen passer stadig, for vi har taget den fjerde rod af to lige store størrelser).	= (1+r)
Vi udregner og hæver parentesen	2 = 1+r
Vi trækker 1 fra på begge sider	2 - 1 = r
Vi trækker 1 fra på begge sider	1 = r

Konklusion: Rentefoden er 1 = 100%

Det kan yderligere bemærkes:

Den årlige fremskrivningsfaktor (1+r ) er 2 (Dvs. gælden fordobles hvert år.)
Den 4-årige fremskrivningsfaktor er 16

Gælden vokser med 1500% på 4 år, nemlig (16-1)·100%

Ovenstående beregning er lavet under forudsætning af, at rentefoden er konstant.

Hvis rentefoden ikke er konstant, kan vi alligevel lave ovenstående beregning.

Den værdi r , vi beregner på ovenstående måde, kaldes:

Den gennemsnitlige rentefod

Eller:

Den gennemsnitlige vækstrate

Eller:

Den gennemsnitlige procentvise ændring.

Dvs. hvis vækstraten havde været konstant lig den gennemsnitlige vækstrate i alle terminer, ville vi få den samme slutværdi.

Eksempel 2:

Benzinprisen er i løbet af 3 år steget fra 10,00 kr. pr. liter til 13,31 kr. pr. liter.

Den procentvise prisstigning har været forskellig fra år til år, så det giver ingen mening at beregne den årlige vækstrate, men vi kan beregne den gennemsnitlige årlige vækstrate.

Den 3-årige fremskrivningsfaktor er: ^13,31/_10,00= 1,313

Altså (1+r)³ = 1,131, idet r er årlig gennemsnitlig vækstrate.

Den ét-årige gennemsnitlige fremskrivningsfaktor er (1+r) = = 1,10

Konklusion: Den gennemsnitlige årlige vækstrate for prisen er 10%

Man kan ikke beregne gennemsnitlig vækstrate ~~ved blot at lægge de forskellige vækstrater sammen og dividere med antallet af terminer~~.

Eksempel 3:

100 kr forrentes gennem 2 år.

Det første år er den årlige rente 20% og den næste år er den årlige rente 80%.

Den gennemsnitlige fremskrivningsfaktor er = 1,47

Den gennemsnitlige procentvise ændring er 47% og ikke ~~(20%+80%)/2= 50%~~

Antal terminer n

Hvis antallet af terminer n er eneste ukendte størrelse, kan n findes ved at gætte systematisk, eller ved at benytte Guide & CAS i RegneRobot, hvilket er tilladt til eksamen.

Vi skal senere i forløbet se, hvordan n kan bestemmes ved almindelig beregning.

2) Se video. Link: gennemsnitlig_rente / %-vis ændring

3) Løs øvelse. Link: Rentesregning

4) Løs E-opgaver: Link: E-opgaver_07_rente_og_gns_rente.htm

5) Løs fra 2006-opgavehæftet 1.001 og 1.002

Benyt RegneRobot med link til opgavehæftet.

Klik i opgavenummeret og se en demo-video.

Link til RegneRobot & opgavehæfte

Skabelon til løsning af 1.001

a) Værdien af et maleri er oprindelig 6000 kr. Det stiger med 13% om året. Værdien efter 12 år skal bestemmes
Jeg vil benytte renteformlen: K=Ko*(1+r)^n
Værdien af maleriet efter 5 år:	60000 *1,12^5 kr	=
11 årig fremskrivningsfaktor:	F=125000/85000	=
Gennemsnitlig årlig fremskrivningsfaktor:	a=F^(1/11)	=
Gennemsnitlig årlig %-vis vækst:	(a-1 )*100%	=

Lektion 8: Indeks

Udfør følgende 5 punkter

1) Se: Video: Indeks

2) Læs:
Her følger en oversigt over prisen på blyfri benzin gennem nogle år. Priserne er angivet i 1990-kr. (faste priser).

år	1993	1994	1995	1996	1997	1998	1999	2000	2001	2002	2003	2004
kr.	5,02	5,09	5,39	5,75	5,78	5,5	6,04	6,79	6,46	6,33	6,18	6,49

Det ses, at priserne både er steget og faldet, men steget mest. For at få et mere overskueligt overblik over prisændringerne, har man indført indekstal.

Man udvælger et år, som kaldes basisåret, og her sættes indeks til 100.

Indeks for de øvrige år findes ved at fremskrive 100 med samme fremskrivningsfaktor, som priserne fremskrives med. Man må således beregne denne fremskrivningsfaktor.

Lad os finde indeks for 1999 med 1993 som basis år.

Dvs. indeks i 1993 er 100.

Fremskrivningsfaktoren for benzin-prisen fra 1993 til 1999 er ^6,04 / _5,02

Indeks for 1999 bliver således 100 · ^6,04 / _5,02 = 120,3… = 120.

Alle indekstal ses nedenfor:

år	1993	1994	1995	1996	1997	1998	1999	2000	2001	2002	2003	2004
kr.	5,02	5,09	5,39	5,75	5,78	5,5	6,04	6,79	6,46	6,33	6,18	6,49
Indeks	100	101	107	115	115	110	120	135	129	126	123	129

Man bemærker, at det er let at få overblik over prisudviklingen ved at kigge på indeks.

Fra 2003 til 2004 er stigningen i indeks: 129 – 123 = 6.
Man siger stigningen har væres 6 procentpoint eller 6 point.

Men bemærk, den %-vise stigning i samme periode er: (¹²⁹/₁₂₃ -1)·100% = 4,9%

Hvis man kender indeks-tal svarende til et basisår, kan indekstal svarende til et andet basisår beregnes.

3) Løs interaktiv øvelse. Øvelse i indeks Formler

4) Løs E-opgaver: E-opgaver 08 indeks.htm

5) Løs fra 2006-opgavehæftet 2.009

Link til RegneRobot & opgavehæfte

Lektion 9a: Geometri, vinkler, areal af trekant og
ensvinklede trekanter

Udfør følgende 4 punkter

1) Se rapportopgaven lige nedenfor.

Du vil formentlig ikke vide hvordan den skal besvares. Meningen er da også, at den skal motivere dig til at lære geometri. Du skal, når du læser det følgende, hele tiden tænke på, om det, du læser, kan bruges til besvarelse af rapportopgaven.
Du skal ikke besvare rapportopgaven før punkt 4)

Rapportopgave ”Find Højden”

(Kan gerne løses af grupper på 2 eller 3)

Find højden på en flagstang, en mast eller en bygning.

Beskriv her mindst 2 metoder til at finde højden.

Nævn fordele og ulemper ved de forskellige metoder.

Vælg på baggrund heraf metode.

Gør rede for nødvendigt værktøj ved den valgte metode, fx målebånd:.

Foretag de nødvendige målinger og find højden.

Beskriv hele forløbet og evaluer projektet.

2) Læs
I denne lektion gennemgås en række begreber og regler, som er nyttige ved geometriske beregninger.

Præcise definitioner og argumenter vil blive behandlet i en senere lektion.

Vinkler

Vinkler måles i grader:

En spids vinkel er under 90°

En ret vinkel er 90°

(Ofte markeres en ret vinkel

med et lille kvadrat)

En stump vinkel er mellem 90° og 180°

En lige vinkeler180°

(Man kan også måle vinkler i radianer. 180° = π radianer og π = ca 3,14)

Tre punkter fx A, B og C fastlægger en vinkel, der fremkommer

ved at tegne fra A til B og videre til C.
B er vinklens toppunkt. Se tegning.

Vinklen betegnes vinkel ABC eller ÐABC

Trekanter og højder i trekanter

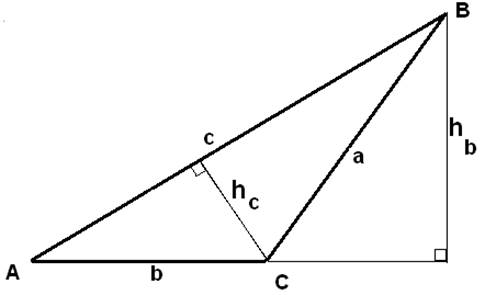
Ovenstående trekant er fastlagt ved punkterne A, B og C.

En trekant, der er fastlagt ved tre punkter A, B og C kan betegnes ∆ABC.

En side i en trekant navngives almindeligvis med samme bogstav som vinklen overfor, men med et lille bogstav.

Højden på c h_cog højden på b h_b er indtegnet.

Vinkel B i trekant ABC betegnes ofte vinkel ABC eller ÐABC

Vinkel A i trekant ABC betegnes ofte vinkel CAB eller ÐCAB

Vinkelsummen i en trekant er altid 180°

Areal af en trekant

Arealet af en trekant er ½ højde · grundlinje

(hvor grundlinjen er siden vinkelret på højden)

Arealet = ½h_a· a = ½h_b· b = ½h_c· c

Bemærk h_aer ikke indtegnet

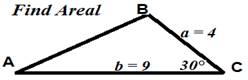
Formler

Areal:
(T er areal,
h_a er højden på a,
h_ber højden på b
og h_c er højden på c)

T = 0,5·a·h_a = 0,5ab·Sin C

T = 0,5·b·h_b = 0,5bc·Sin A

T = 0,5·c·h_c = 0,5ca·Sin B

Herons formel:

hvor

Eksempel:

T = 0,5·4·9·Sin(30°) = 0,5·4·9·0,5 = 9

Ensvinklede trekanter

To trekanter kaldes ensvinklede, hvis vinklerne er parvis lige store.

Enten er de to trekanter præcis ens eller også er den største en forstørrelse af den mindste.

Ved 2 ensvinklede trekanter defineres skalafaktoren som den faktor, man skal gange sidelængderne med i den ene trekant for at få sidelængderne i den anden.

Hvis de to trekanter er præcis ens, så er skalafaktoren 1.

Hvis skalafaktoren er mellem 0 og 1, så er der faktisk tale om en formindskelse.

Hvis man kender længden på tilsvarende sider i de 2 trekanter, så kan skalafaktoren beregnes. Nedenfor ses 2 ensvinklede trekanter.

Der gælder: skalafaktoren = ⁶/₄(Kaldes også forstørrelsesfaktoren)

Nogen gange benyttes ordet forstørrelsesfaktor i stedet for skalafaktor.

Se regler for areal af trekanter og for ensvinklede trekanter i formelsamlingen

3) E-opgaver: E-opgaver_9a_ensv.retv.trek.htm

4) Skriv rapportopgave Klik her og skriv rapporten ind i skemaet.

Det kan være en hjælp at se denne video: Find-hoejden

Link: Indholdsfortegnelse

Lektion 9b: Geometri, retvinklede trekanter, Sinus, Cosinus & Tangens

Udfør følgende 3 punkter

1) Læs

Hvis den ene vinkel i en trekant er 90°, så kaldes trekanten retvinklet.

En ret vinkel markeres ofte med et lille kvadrat.

Siden over for den rette vinkel kaldes hypotenusen.

De 2 andre sider kaldes kateter.

Sinus, Cosinus og Tangens

Hvis man kender 2 sider i en retvinklet trekant, kan man beregne de spidse vinkler ved at benytte Sinus, Cosinus og Tangens på lommeregneren, forkortet: Sin, Cos og Tan.

Til enhver spids vinkel er knyttet et tal vi kalder Sinus til vinklen.

Også til Cosinus og Tangens er knyttet et tal til enhver spids vinkel og der gælder:

Sinus til en spids vinkel i en retvinklet ∆ er modstående katete divideret med hypotenusen.

Cosinus til en spids vinkel i en retvinklet ∆ er hosliggende katete divideret med hypotenusen

Tangens til en spids vinkel i en retvinklet ∆ er modstående katete divideret med hosliggende katete.

Definitionen af Sinus, Cosinus og Tangens kommer i en senere lektion.

Sammenhængen mellem sider og vinkler kan udtrykkes således:

Sin v = ^{modstående
katete} / _hypotenusen

Cos v = ^{hosliggende
katete} / _hypotenusen

Tan v =^{modstående katete} / _{hosliggende katete}

Når man kender Sin, Cos eller Tan til en vinkel, kan selve vinklen findes ved hjælp af ArcSin, ArcCos eller ArcTan, som på de fleste lommeregnere betegnes med sin^-1. (Tast først 2nd og derefter Sin. )

På nogle lommeregnere tastes inv i stedet for 2nd.

Hvis man kender en vinkel og en side i en retvinklet trekant kan de øvrige sider beregnes ved at betragte ovenstående formler som ligninger.

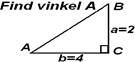
Eksempler:

Sin(30°)=^b/₈Dvs b = 8·Sin(30°) = 8·0,5 = 4

Tan(A)= ²/₄ = 0,5 Dvs Vinkel A = 26,6° (Benyt Tan^-1 eller ArcTan)

Se regler for Sinus, Cosinus og TAngens i formelsamlingen

2) E-opgaver: E-opgaver 9b geometri

3) Løs fra 2006-opgavehæftet 1.021, 1.022 Facitliste

Link til RegneRobot & opgavehæfte

Link: Indholdsfortegnelse

Lektion 9c: Geometri, retvinklede trekanter, Pythagoras’ sætning

Udfør følgende 4 punkter

1) Se video. Link: Geometri

2) Læs

Pythagoras’ sætning

Kvadratet på hypotenusen = summen af kateternes kvadrat.

Det er sædvane at navngive trekantens hjørnepunkter med store bogstaver.

Siden over for hvert hjørnepunkt navngives oftest med det tilsvarende lille bogstav

Hvis trekantens vinkelspidser får bogstav-navnene A, B og C, hvor C er den rette vinkel, så kan pythagoras’ sætning udtrykkes således:

c² = a² + b²

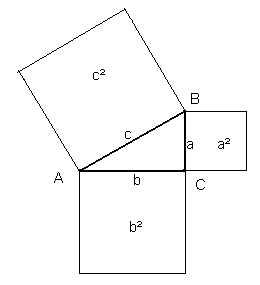
Hvis man kender to sider i en retvinklet trekant, kan man beregne den tredje side

ved at indsætte de kendte størrelser i Pythagoras’ sætning, og eventuelt løse en ligning.

Se regler for retvinklede trekanter i formelsamlingen

2) Løs interaktivt Opgaver i retvinklede trekanter

3) E-opgaver: E-opgaver 9c geometri

4) Løs fra 2006-opgavehæftet 1.023, 1.024, 1.025 Facitliste

Link til RegneRobot & opgavehæfte

Lektion 9d: Geometri, vilkårlige trekanter

Udfør følgende 3 punkter

1) Læs

Vilkårlige trekanter

Ikke alle trekanter er retvinklede. Følgende formler gælder for enhver trekant ABC uanset om den er retvinklet eller ej.

Sinusrelationerne:

Cosinusrelationerne:
(Også kaldet den
udvidede Pythagoras)

c² = a² + b² – 2ab·Cos C

b² = a² + c² – 2ac·Cos B

a² = b² + c² – 2bc·Cos A

Cos C =

Cos B =

Cos A =

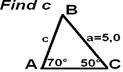
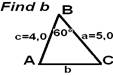
Eksempler:

Sin(70°) 5,0	=	Sin(50°) c	Dvs c =	5,0·Sin(50°) Sin(70°)	= 4,0

b² = 5,0² + 4,0² – 2·4,0·5,0·Cos(60°) =21,0 Dvs B =

= 4,6

Hvornår bruges hvilke formler ved trekantberegning ?

Kig efter, om der er ensvinklede trekanter

Vurder om Areal-formlen kan bruges

Hvis de 3 vinkler er i spil, så: Vinkelsum ( i spil betyder er kendt eller ønskes beregnet)

Hvis 2 vinkler og de modstående sider er i spil, så Siusrelationerne.

Hvis alle 3 sider og en vinkel er i spil, så Cosinusrelationerne

Ved retvinklede trekanter:

Hvis kun sider er i spil: Pythagoras

Hvis en vinkel og 2 kateter er i spil: Tangens

Hvis hosliggende katete ikke er i spil: Sinus

Ellers: Cosinus

Se regler for geometri i formelsamlingen

2) E-opgaver: E-opgaver 9d geometri

3) Løs fra 2006-opgavehæftet 1.026 og 2.005 Facitliste

Link til RegneRobot & opgavehæfte

Lektion 9e: Geometri, Sinus, Cosinus og Tangens i regneark

Udfør følgende 3 punkter

1) Læs

Sinus, Cosinus og Tangens kan være lidt vanskelige for dig at bruge i regneark, så undgå det. Brug hellere RegneRobot.

I regneark benyttes ikke grader som vinkelmål, men en anden måleenhed til vinkler, der kaldes radianer. I RegneRobot benyttes grader ligesom på de fleste lommeregnere.

180º = π radianer. (π er ca. lig 2,7 )

Som regel udelades radianer og man kan skrive 180º = π

I videregående matematik anvendes ofte radianer.

Hvis man kender en vinkel i grader, kan den konverteres til radianer ved at
gange med ^π/180 .

De omvendte funktioner til Sin, Cos og Tan betegnes på de fleste lommeregnere:

Sin^-1,Cos^-1 og Tan^-1. I regneark betegnes de ArcSin, Arccos og ArcTan.

I RegneRobot kan man benytte begge slags betegnelser.

2) E-opgaver: E-opgaver 9e geometri

3) Løs 1.027, som er her:

Opgave 1.027

Bestem a og vinkel B i trekant ABC,
hvor vinkel A er 94°, b=3 og c=5

Link til RegneRobot

Lektion 10a: Sammenhæng mellem variable

Udfør følgende 6 punkter

Rapportopgave ”Temperatur”

Rapportopgaven skal først løses under punkt 6) efter du har gennemgået denne lektion.

Hr. Olsen overvejer at emigrere til enten Palermo i Italien eller Antalya i Tyrkiet. Hans valg afhænger af klimaet de to steder.

Ved hjælp af Internettet skal du finde gennemsnitstemperaturen på forskellige årstider både i Palermo (Italien) og i Antalya (Tyrkiet).

Opgaven går ud på at finde ud af, hvor det er varmest om sommeren, og hvor det er varmest om vinteren. Der ønskes bl.a. en grafisk fremstilling af temperaturforholdene.

Det vil være naturligt at søge fx på google.dk eller DMI.dk

Rapporten skal mindst indeholde følgende afsnit:

§ Indledning med opgaveformulering eller rapportens formål.

§ Beskrivelse af arbejdsforløb.

§ Fremvisning af resultaterne og en forklaring med vurdering af klimaforholdene de 2 steder.

§ Afslutning med fx en anbefaling og evaluering af projektet.

2) Læs

Variable

I matematik taler vi ofte om variable talstørrelser. Det kan fx være temperaturen målt i celsius-grader, der varierer i løbet af året. En talstørrelse, der varierer kaldes en variabel.

Et kvadrat er en firkant hvor alle vinkler er 90° og alle sider lige lange.

Lad os tegne et kvadrat på et stykke papir, der er 7,5 cm på hver led.

Hvis vi regner i cm, kan sidelængden variere fra 0 og op til 7,5.

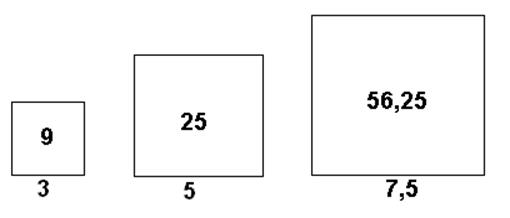
Arealet kan variere fra 0 og op til 56,25.

Arealet af kvadratet afhænger af sidelængden og kaldes den afhængige variable mens sidelængden kaldes den uafhængige variable.

Hvis vi kalder arealet y og sidelængden x, bliver arealet y bestemt ved regneforskriften: y = x² (x² betyder x∙x, fx 5² betyder 5∙5) .

Funktion

Man siger, at arealet y er en funktion af x.

Det skrives y = f(x) og udtales ”y er lig f af x”

Regneforskriften kan også skrives f(x) = x².

Funktionen er defineret for alle tal x i intervallet 0 til og med 7,5.

Mængden af de tal x, hvor funktionen er defineret kaldes definitionsmængden.

Definitionsmængden for en funktion med navnet f kan forkortet skrives Dm(f)

Ud fra regneforskriften f(x) = x² får vi

Hvis x er 3 så er y = f(3) = 3² = 9 og hvis x er 4 så er y = f(4) = 4² = 16

Vi siger funktionsværdien af 3 er 9 og funktionsværdien af 4 er 16

Mængden af alle funktionsværdierne kaldes værdimængden for f og er intervallet fra 0 til og med 56,25..

Værdimængden for en funktion med navnet f kan forkortet skrives Vm(f)

Grafen for en funktion

Ofte vil man præsentere en funktion grafisk.

Hvis man vil tegne funktionen med regneforskriften y = x² , er det en god ting at starte med at udfylde et såkaldt sildeben med forskellige samhørende
x- og y-værdier, såkaldte støttepunkter:

Selvom 0 ikke tilhører definitionsmængden, kan det være praktisk at have 0 med i sildebenet, men vi skriver 0 i parentes: ( 0). Den tilsvarende y-værdi, som også er 0 sættes ligeledes i parentes.

Støttepunkter for y = x².

	x	( 0 )	0,5	1	4	6	7,5
	y	( 0 )	0,25	1	16	36	56,25

Den første og sidste x-værdi er de to endepunkter i definitionsintervallet. Resten af x-værdierne er valgt så de fordeler sig nogenlunde jævnt i definitionsmængden.

Når man skal tegne en graf vælger man selv x-værdier.

Vi vil tegne et billede (en graf) af funktionen i et såkaldt koordinatsystem.

Et koordinatsystem består af 2 tallinjer vinkelret på hinanden.
Den ene tallinje kaldes x-aksen og den anden y-aksen.

Hvert støttepunkt plantes ud for sin x-værdi på x-aksen og ud for sin y-værdi på
y-aksen.

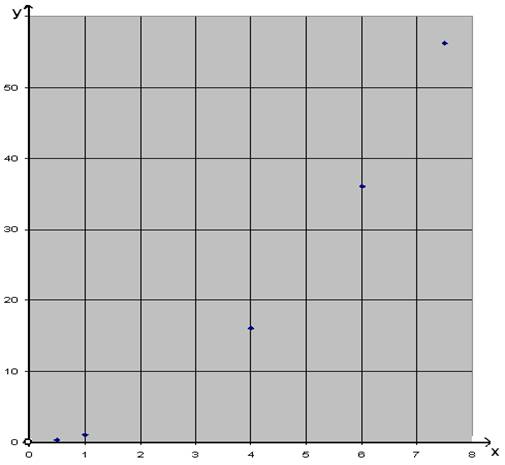
Punktet med x-værdien 0 er afsat med en ring fordi 0 ikke ligger i definitionsmængden. De øvrige punkter ligger på den graf vi vil tegne.

Når vi skal tegne grafen, vil vi som regel vælge at tegne en blød kurve gennem støttepunkterne:

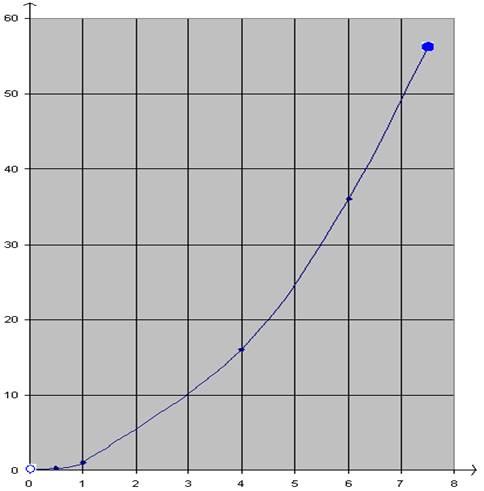
Ved at forbinde grafpunkterne med en blød kurve antager vi, at vi har tegnet de punkter, hvor y = x² , idet x for hvert punkt er punktets placering ud for x-aksen, mens y er punktets placering ud for y-aksen.

Denne antagelse giver imidlertid ikke et præcist billede af grafen. Fx ser det overfor ud som om f(x) er 10; men f(3) er faktisk 9.

Ethvert punkt i koordinatsystemet er bestemt ved et talar (x, y) der kaldes punktets koordinatsæt.

x er punktets placering ud for x-aksen (også kaldet 1. aksen) og kaldes punktets x-værdi (eller punktets 1. koordinat).
y er punktets placering ud for y-aksen (også kaldet 2. aksen) og kaldes punktets y-værdi (eller punktets 2. koordinat).

Fx er (5 , 2.5) punktet ud for 5 på x-aksen og ud for 2.5 på y-aksen (Der er brugt decimalpunktum i stedet for decimalkomma. Det gøres ofte.)

I punktet (0 , 0) er tegnet en ring. Det betyder, at punktet ikke hører med til grafen..

I punktet (7.5 , 56.25) er tegnet en bolle. Det betyder, at punktet hører med til grafen.

3) Se videoen: Funktioner og grafisk løsning

4) Løs E-opgaver E-opg 10a variable

5) Aflever rapportopgaven ”Temperatur”

Se punkt 1)

6) Løs fra 2006-opgavehæftet 1.004 Facitliste

Lektion 10b: Sammenhæng mellem variable

Udfør følgende 5 punkter

1) Læs

Proportionalitet

”Ligefrem proportional” eller blot ”proportional”

Hvis man køber benzin til 10 kr pr. liter, vil prisen i kroner være 10 gange så stor som

antal liter.

Hvis antal liter kaldes x og prisen kaldes y, gælder y=10x.

Vi siger y er proportional eller ligefrem proportional med x og at proportionalitetsfaktoren er 10.

For x≥0 ser grafen for y således ud:

Omvendt proportionalitet

Hvis vi har 420 havefliser og vil lave en terrasse kan vi fx lægge 42 fliser på den ene led og 10 fliser på den anden.

Terrassen er et såkaldt rektangel. Se tegningen, hvor x = 42 og y = 10.

y = 10

x = 42

Vi kan også vælge at lægge 21 fliser på den ene led og 20 på den anden.

Se tegning, hvor x = 21 og y = 20.

y = 20

x = 21

Viser at når y gøres dobbelt så stor, så bliver x halv så stor.

Endvidere gælder, at hvis vi havde gjort y tre gange så stor altså til 30 så ville x blive tre gange så lille, nemlig 14.

Vi kunne også gøre x dobbelt så stor til 84, men så måtte vi også gøre y dobbelt så lille, nemlig 5.

Generelt gælder der følgende sammenhæng mellem x og y:

x·y = 420

Vi siger y og x er omvendt proportionale med proportionalitets-faktoren 420.
For x mellem 1 og 10 ser grafen for y således ud:

I ovenstående tilfælde med fliser er x større end nul.

Bemærk: Regneudtrykket har ingen mening for x lig nul; men

man kan godt beregne værdien af udtrykket for negative x.

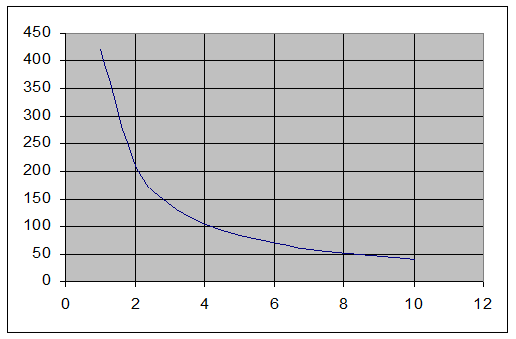
For x forskellig fra nul ser grafen for y således ud:

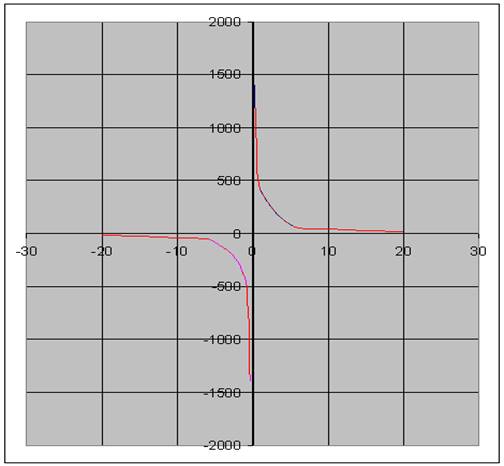
Bemærk: Ovenstående illustrerer ikke flise-eksemplet, hvor x > 0 ; men blot regneforskriften:

Intervaller

Ofte vil definitionsmængden og værdimængden være intervaller.

Ved intervaller benyttes nogle matematiske symboler, hvis betydning fremgår af følgende eksempler:

Interval- eksempel	Forklaring	Grafik
] -∞ , 3[	Åbent interval bestående af alle tal mindre end 3
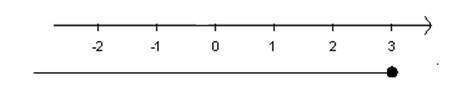
] -∞ , 3]	Halvåbent interval bestående af alle tal mindre end eller lig med 3
]-2 ; 2,3[	Åbent interval bestående af alle tal mellem -2 og 2,3
[-2 ; 2,3[	Halvåbent interval bestående af alle tal større end eller lig -2 og mindre end 2,3
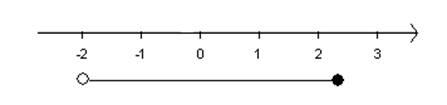
]-2 ; 2,3]	Halvåbent interval bestående af alle tal større end -2 og mindre end eller lig 2,3
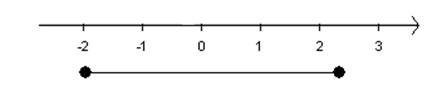
[-2 ; 2,3]	Lukket interval bestående af alle tal større end eller -2 og mindre end eller lig 2,3
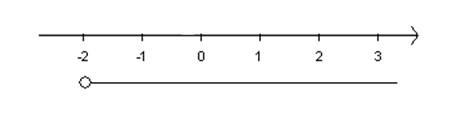
]-2 ; ∞[	Åbent interval bestående af alle tal større end -2
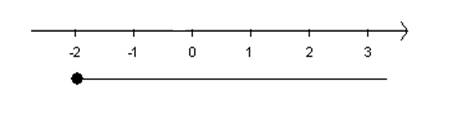
[-2 ; ∞[	Åbent interval bestående af alle tal større end eller lig -2

2) Opgaver (Der er facitliste sidst i denne lektion)

Betragt nedenstående graf for funktionen f og løs de følgende opgaver

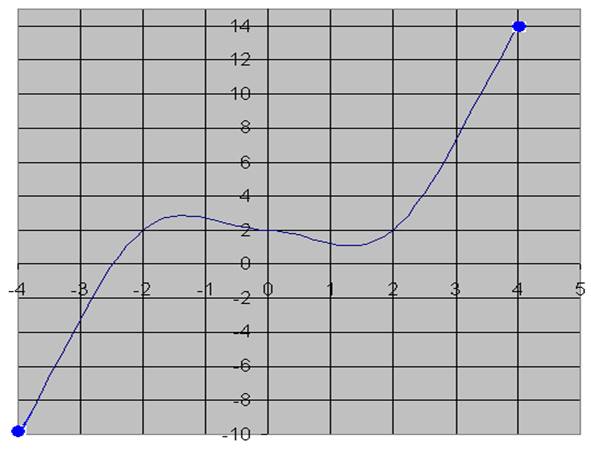
Opgave 1

Udfyld de tomme felter

	x	-4	-2	0	2
	*y = f(x)*					14

Opgave 2

Find f(-2)

f(-2) =

Opgave 3

Løs ligningen: f(x)=14

x =

Opgave 4

Løs ligningen: f(x)=2 Der er 3 løsninger, som kan skrives i en tuborg-parentes, også kaldet mængdeklamme og adskilles med komma.

Løsningsmængden =

{ , , }

Opgave 5

Hvad er definitionsmængden?

Dm(f) =

Opgave 6

Hvad er værdimængden?

Vm(f) =

Facits:

Opgave 1

x	-4	-2	0	2	4
*Y=f(x)*	-10	2	2	2	14

Opgave 2

Find f(-2): f(-2) =2

Opgave 3

Løs ligningen: f(x)=14: x=4

Opgave 4

Løs ligningen: f(x)=2 Der er 3 løsninger, som kan skrives i en tuborg-parentes.

Løsningsmængden = {-2, 0, 2}

Opgave 5

Dm(f) = [-4; 4]

Opgave 6

Vm(f) = [-10; 14]

3) Løs interaktiv opgave. Link: Proportionalitet

4) Løs E-opgaver E-opg 10b Proportionalitet

5) Løs fra 2006-opgavehæftet 1.007, 1.09 og 2.003 Facitliste

Link til RegneRobot & opgavehæfte

Link: Indholdsfortegnelse

Lektion 11: Lineære funktioner

Udfør følgende 5 punkter

1) Se: Video med lineær funktion

2) Læs:

Definition:
En lineær funktion er en funktion, hvor grafen er lineær.
Dvs. grafen er en ret linje eller en del af en ret linje.
Her ses et eksempel på en lineær funktion

Eksempel 1:

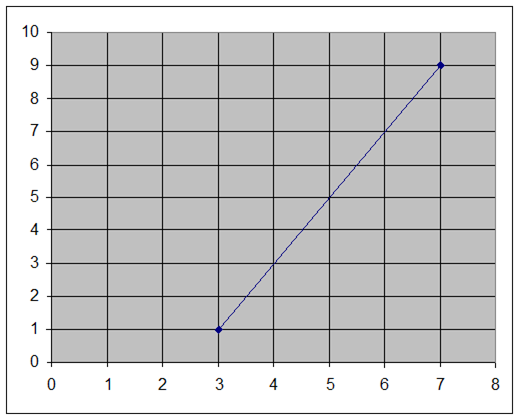
Funktionen er defineret i intervallet [3; 7]

Eksempel 2
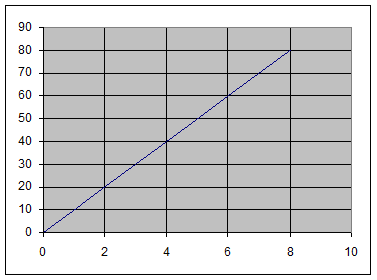
I lektion 1 så vi et eksempel på en taxa der kostede 25 kr i startgebyr og 12 kr pr km.
Prisen kan beregnes ud fra formlen eller regneforskriften: f(x) = 12x + 25.
Grafen for f ser således ud:

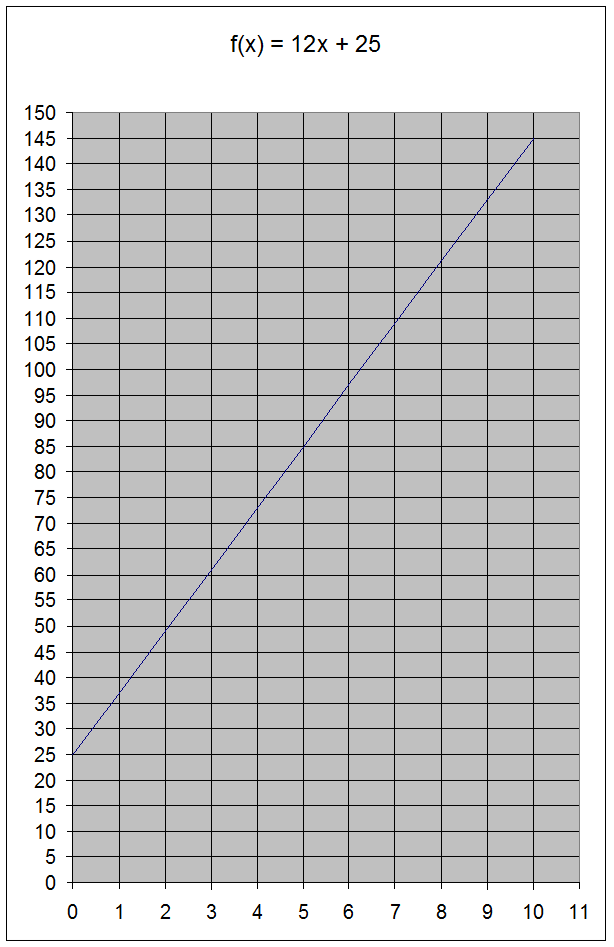
Vi ser grafen bliver lineær. Derfor er f en lineær funktion.

Hældningskoefficient
Af grafen kan man fx aflæse, at x-værdien 5 giver y-værdien 85. Vi skriver f(5)=85.
Hvis vi gør x-værdien én større til 6, kan vi af grafen aflæse, at funktionsværdien forøges med 12 svarende til, at én ekstra km koster 12 kr mere.

Vi bemærker, ligegyldigt hvor langt vi har kørt, så vil en ekstra km koste 12 kr mere.

Man kan bevise, at for lineære funktioner gælder generelt: Ligegyldigt hvilken x-værdi, man betragter, så vil y vokse med samme tal, hvis x gøres én større og dette tal kaldes hældningskoefficienten.

Definition:
Hældningskoefficienten er ændringen i y når x bliver én større.
Hældningskoefficienten kaldes ofte a.
Hvis a > 0 (større end nul), så er funktionen voksende.
Hvis a < 0 (mindre end nul), så er funktionen aftagende.

Hvis a = 0 , så er funktionen konstant og grafen vandret, altså parallel med første-aksen.

Begyndelsesværdi

Såfremt en funktion er defineret for x=0, kaldes f(0) begyndelsesværdien og den kan aflæses på y-aksen.
Hvis funktionen ikke er defineret for x=0, taler vi alligevel om en begyndelsesværdi.

Definition:
Begyndelsesværdien er det tal på y-aksen, hvor grafen eller dens forlængelse
skærer y-aksen.

Regneforskrift
Man kan bevise, at de lineære funktioner er dem, der kan skrives med en regneforskrift af formen y = ax + b, hvor

b er begyndelsesværdien.

a er hældningskoefficienten eller bare linjens hældning.

a er det stykke grafen løfter sig når x bliver én større.

Hvis grafen går nedad bliver a negativ. Funktionen er aftagende.

I eksemplet med taxaen er a= 12 og b=25.

Hvis man til to x-værdier kender de tilsvarende y-værdier for en funktion, kan man finde regneforskriften. Metoden er først at finde a og derefter b.

Lad y₁ betyde funktionsværdien af x₁ og y₂ funktionsværdien af x₂.

Der gælder følgende formler:

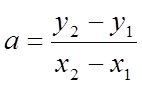, hvor y₁ = f(x₁) og y₂= f(x₂)

Når man har beregnet a og b kan regneforskriften umiddelbart opskrives. Lad os se et eksempel.

Vi vil finde regneforskriften for funktionen i eksempel 1.

Af grafen kan vi aflæse følgende x- og y-værdier :

x	3	7
y	1	9

Vi bruger formlerne og får

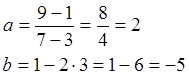
Dvs. regneforskriften bliver y = 2x - 5
Hvis vi kalder funktionen g, kan vi skrive: g(x) = 2x – 5 , Dm(g) = [3; 7]

Det er god orden at anføre definitionsmængden, når regneforskriften opskrives.

3) Løs Interaktivt: Opgaver i lineær funktion

4) Løs E-opgaver: E-opg. 11 Lineær funktion

5) Løs fra 2006-opgavehæftet 2.002, 2.012 Facitliste

Link til RegneRobot & opgavehæfte

Link: Indholdsfortegnelse

Lektion 12: Tegn grafer med pc

Udfør følgende 3 punkter

1) Læs:

Sådan tegnes grafer med pc

Her vil blive gennemgået 3 måder til tegning af grafer med pc:

· Ved hjælp af regneark Excel

· Ved hjælp af Graph, som kan downloades gratis via padowan.dk/download

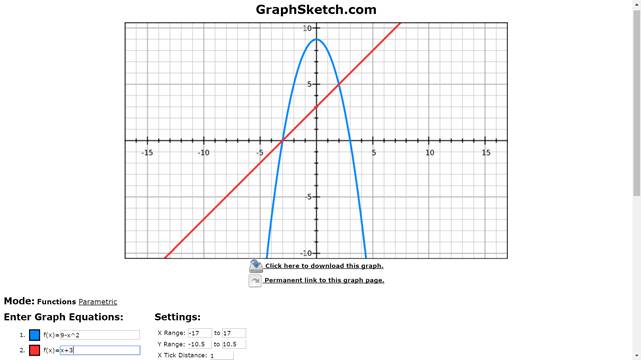
· Ved hjælp af GraphSketch.com , der er gratis og online, men også kan downloades.

Du behøver ikke at fordybe dig i alle 3 metoder. Du skal blot kunne tegne grafer på den ene eller anden måde. Start med at prøve GraphSketch.com , som er meget let at betjene.

Fordele og ulemper ved de 3 metoder:

	Fordele	Ulemper
Regneark Excel	Praktisk, hvis man i forvejen arbejder i Excel.	Besværligt
Graph	Mange faciliteter. På dansk	Lidt vanskeligt at betjene. Man skal bruge punktum i stedet for decimalkomma. Virker ikke på alle computere. Hvis du fx skriver ”1/2x”, så bliver det opfattet som ^”^” i stedet for ^” ^”.
GraphSketch.com	Meget let at betjene. Ingen installation. Virker på næsten alle computere	På engelsk Man skal bruge punktum i stedet for decimalkomma. skrives i GraphSketch root(a,n), altså omvendt rækkefølge.

Tegn grafer med regneark Excel

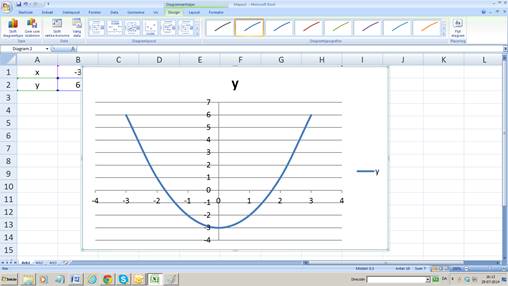
Vi vil tegne grafen for y=x²-3 og starter med at lave en tabel med støttepunkter i regnearket.

Du udfylder nogle celler i regneark fx således: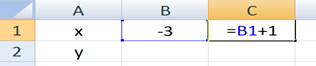

Når du taster Enter kommer der til at stå -2 i celle C1.

Du markerer cellerne C1 til H1:

Tast Ctrl+r og du får gentaget metoden fra C2 mod højre i det markerede område sådan:

I celle B3 skriver du: =B1^2-3 og derved bliver funktionsværdien af -3 beregnet.

Du markerer cellerne B2 til H2 og taster Ctrl+r og får:

Nu har du fået en tabel med støttepunkter og er klar til at tegne grafen.

Du markerer C1 til H2, og i fanebladet Indsæt vælger du og sådan:

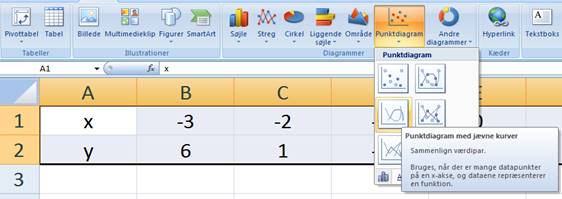
Og vupti, så popper grafen frem:

Vinduet med grafen kan flyttes med musen og det kan kopieres.

Tegn grafer med gratisprogrammet Graph

Link til gratis download af Graph: http://www.padowan.dk/download/

Du klikker i SetupGraph-4.4.2.exe (9.6 MB)

Gratisprogrammet bliver installeret på din pc, og du får dette ikon på dit skrivebord:

Du klikker i ikonet og får dette skærmbillede:

Herefter kan du øverst til venstre klikke i og der popper en dialogboks op, som du fx kan udfylde således:

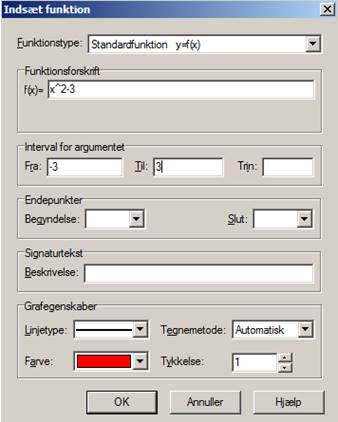
Når du har klikket OK kommer følgende skærmbillede med grafen:

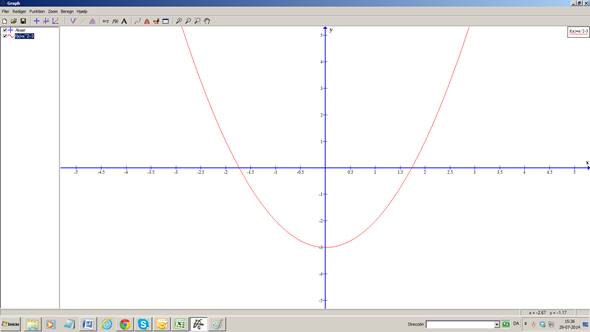
Hvis din graf ikke kommer frem, kan det skyldes, at grafen ligger uden for vinduet.

Du kan ændre tallene på akserne ved at klikke i næsten øverst til venstre.

Du finder selv ud af flere muligheder ved at prøve dig frem og benytte hjælp.

Tegn grafer online med, GraphSketch.com som er gratis.

Skråt til venstre under koordinat-systemet skriver du regneforskrift for de funktioner, der skal tegnes, og du taster Enter.

Hvis graferne ikke kommer, kan det skyldes, at de er uden for vinduet.

Du kan ændre tallene på akserne lige under koordinatsystemet.

2) Løs E-opgaver: E-opg. 12 Regneark

3) Løs fra 2006-opgavehæftet 1.005, 1.010, 1.012 Facitliste

Link til RegneRobot & opgavehæfte

Lektion 13: Logaritmer

Udfør følgende 3 punkter

1) Se video Link: Logaritme

2) Læs:

10-talslogaritmen

Ligningen 4^x = 35 kan være vanskelig at løse fordi x er eksponent; men her er hjælp at hente hos logaritmefunktionen, som vi skal lære om nu.

10-talslogaritmen til et positivt tal er den eksponent, man skal sætte på 10 for at få tallet.

Fx: 10-talslogaritmen til 100 er 2 , fordi 10² = 100.

Ofte siger man blot logaritme i stedet for 10-talslogaritme.

Logaritmen til et tal x skrives Log(x) eller blot Log x, og bemærk x skal være positivt.

Logaritmeregler:

log(a · b) = log(a) + log(b) og log(a^x) = x log(a)

Det er den sidste af disse to regler, der udnyttes til løsning af visse ligninger.

Eks. 1

Løs ligningen: 4^x = 35

Løsning:

              4^x   =   35
              Log(4^x)    =   Log(35)

              x ·Log(4) =   Log(35)

x =

x = 2,56464…

x = 2,5646

Eks. 2

Løs ligningen: 3 · 7^x = 90

Løsning

3 · 7^x = 90

7^x = 30 ó
x · Log(7) = Log(30)

x =

x = 1,74786…

x = 1,7479

Løs flere øvelsesopgaver. Link: Eksponentielle ligninger

I lektion 7 blev det lovet, at vi senere skulle se, hvordan man kan beregne n i renteformlen: K=K_o·(1+r)ⁿ, og det er nu, vi skal se det.

Eks. 3

500 forrentedes gennem nogen år med 3% pr år og voksede til 903kr.

Hvor mange år gik der.

Løsning

Vi ved

903 = 500·1,03ⁿ

⁹⁰³/₅₀₀ = 1,03ⁿ

Log( ⁹⁰³/₅₀₀) = Log(1,03ⁿ)

Log( ⁹⁰³/₅₀₀) = n·Log(1,03)

n = 19,9…

n = 20

Der gik 20 år

3) Løs E-opgaver: E-opgaver 13 logaritmer

Lektion 14a: Eksponentielle funktioner

Udfør følgende 4 punkter

1) Læs:

Definition:

En funktion kaldes eksponentiel, hvis den har en regneforskrift, der kan skrives således:

f(x) = b a^x eller y = b a^x , idet a og b er positive tal.

Eksempel 1:

Indiens befolkning var i 1900 ca. 138 millioner, og er siden vokset med ca. 2% om året..

Vi siger, at befolkningstallet hvert år fremskrives med 2%.

Den årlige fremskrivningsfaktor er 1,02

Efter 1 år er befolkningstallet:	138 mio ·1,02 =	140,8 mio
Efter 2 år er befolkningstallet:	138 mio ·1,02² =	143,6 mio
Efter 3 år er befolkningstallet:	138 mio ·1,02³ =	146,4 mio
Efter 4 år er befolkningstallet:	138 mio ·1,02⁴ =	149,4 mio
Efter x år er befolkningstallet:	138 mio ·1,02^x

Befolkningstallet kan beskrives med funktionen f(x) = 138 · 1,02^x

Hvor x er antal år efter 1900

Vi lægger mærke til, at befolkningstallet i Indien vokser eksponentielt (næsten). Vi siger, at befolkningstallet kan beskrives med den eksponentielle model: f(x) = 138 ·1,02^x

Dette minder meget om kapitalfremskrivning, hvor formlen er: K = K₀· (1+r)ⁿ

Læg mærke til, at n er et helt tal ved kapitalfremskrivning, nemlig antallet af rentetilskrivninger (antal terminer).

I regneforskriften for Indiens befolkning behøver x ikke at være et helt tal.

b i regneforskriften kaldes begyndelsesværdien, fordi f(0) = b·a⁰ = b·1 = b

a i regneforskriften kaldes fremskrivningsfaktoren svarende til en tilvækst i x på 1.

Ofte siges blot fremskrivningsfaktoren.

Hvis a er mellem 0 og 1, er f aftagende.

I den eksponentielle model for Indiens befolkning er a = 1,02.

Hver gang, der går ét år, fremskrives Indiens befolkning med 2%.

Man beregner en fremskrivning på 2% ved at gange med 1,02 nemlig den årlige fremskrivningsfaktor.

Den 2-årige fremskrivningsfaktor er 1,02·1,02 = 1,02².

Den 7-årige fremskrivningsfaktor for Indiens befolkning er 1,02⁷

Eksempel 2:

50g radioaktivt stof, der henfalder med 5% om dagen kan beskrives med en eksponentiel funktion. Der er en daglig tilvækst på -5% uanset hvilken dag, der betragtes.

Det er en eksponentielt aftagende funktion og regneforskriften er. y = 50·0,95^x , hvor x er antal dage siden begyndelsen, da der var 50g.

Formlerne for a og b

Hvis man kender 2 funktionsværdier, kan man beregne a ved formlen:

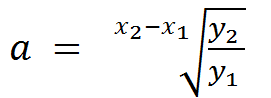
Herefter kan b findes ved hjælp af formlen:

b = y₁ · a^-x¹

eller

b = ^y¹/ a^x¹

Eksempel 3:

x	-2	17
Y	11	0,9

= 0,8766… = 0,877

b = 11·0,8766…^-(-2) = 11·0,8766…^-(-2) = 11·0,8766…² = 8,4519… = 8,452

Regneforskriften bliver således: y = 8,452 · 0,877^x

Bevis for:

Vi er i den situation, at vi kender 2 funktionsværdier y₁ og y₂_,svarende til x-værdierne x₁og x₂_.

Det stiller vi op i et sildeben:

x	x₁	x₂
y	y₁	y₂

Ud fra regneforskriften fås:

y₁ = b · a^x¹ og

y₂ = b · a^x²

Den nederste af de 2 ligninger divideres med y₁

y₂---------
y₁

b · a^x²
-------------------
y₁

y₁ i nævneren til højre erstattes med b · a^x¹ , der har samme værdi.

y₂----------
y₁

b · a^x²
--------------------------
b · a^x¹

Brøken til højre forkortes med b

y₂---------
y₁

a^x²
---------------
a^x¹

Ved hjælp af potensregler for division fås:

y₂---------
y₁

a^x²^-^x¹

Vi tager nu en passende rod på begge sider. Talletx₂-x₁bestemmer hvilken rod vi tager, og vi får:

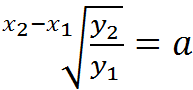hvilket skulle bevises.

Bevis for b = y₁ · a^-x¹ eller b = ^y¹/ a^x¹

Vi bemærker, division med a^x¹er det samme som multiplikation med a^-x¹

De 2 formler er således faktisk ens og blot skrevet på lidt forskellig måde.

Ud fra regneforskriften fås:

y₁ = b · a^x¹ ó ^y¹ / a^x¹ = b hvilket skulle bevises.

Eksempel 4:

Vi betragter 2 funktionsværdier y₁ og y_{2 ,}svarende til x-værdierne x₁og x_2.

x	5	8
y	4	6

a =

= 1,5^(1/3) = 1,1447… = 1,145

b = ⁴/_1,1447…⁵ = 2,0350… = 2,035

og regneforskriften bliver f(x) = 2,035·1,145^x

Herefter kan vi fx beregne

f(10) = 2,035 ·1,145¹⁰

2) Se video: Eksponentiel funktion

3) Løs E-opgaver: E-opg_14a_Eksp_funktion

4) Løs fra 2006-opgavehæftet 1.013 Facitliste

Link til RegneRobot & opgavehæfte

Lektion 14b: Eksponentielle funktioner

Udfør følgende 5 punkter

1) Læs

Tegning af graf for en eksponentiel funktion

Hvis man vil tegne en eksponentiel funktion kan man med fordel benytte et såkaldt enkeltlogaritmisk koordinatsystem. Hertil benyttes enten enkeltlogaritmisk papir eller regneark.

Hvis støttepunkterne flugter en linje i et enkeltlogaritmisk koordinatsystem, kan man konkludere, der med god tilnærmelse er tale om en eksponentiel funktion.

Enkelt-logaritmisk koordinatsystem vil blive forklaret lidt senere.

Eksempel:

Ilt-trykket falder, når man kommer op i bjergene. Her ses nogle måleresultater.

Højde	x	0	500	1000	1500	2000	2500	3000
Ilt-tryk	y	150	140	131	123	115	107	100

Disse er indtegnet nedenfor i et enkeltlogaritmisk koordinatsystem.

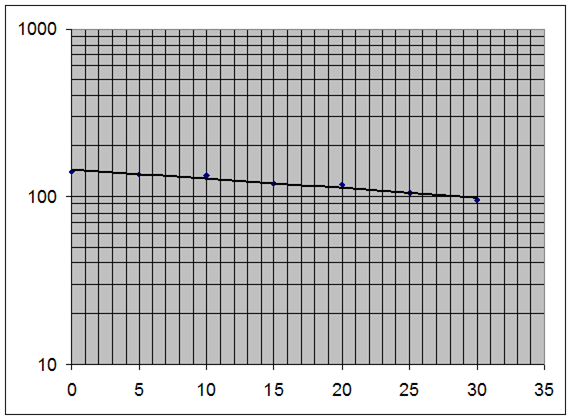
Det ses, støttepunkterne i dette enkeltlogaritmiske koordinatsystem flugter en linje, og vi siger, at ilt-trykket som funktion af højden kan beskrives ved en eksponentiel model.

Enkeltlogaritmisk koordinatsystem

I et enkeltlogaritmisk koordinatsystem er tallene på y-aksen placeret således, at grafen for en eksponentiel funktion bliver lineær, dvs. en ret linje eller en del af en ret linje.

En sådan tal-skala kaldes en logaritmisk skala.

x-aksen er helt sædvanlig i et enkelt logaritmisk koordinatsystem.

Logaritmisk skala

En logaritmisk skala kan defineres på følgende måde.

Tallet 1 placeres et vilkårligt sted på y-aksen.

Ethvert andet positivt tal placeres i afstanden Log(y) over 1 regnet med fortegn, at forstå på den måde, at når Log(y) er negativ, så placeres tallet y under 1.

Bemærk:

For y<1 er Log(y) negativ. y placeres over 1

For y=1 er Log(y) lig nul.

For y>1 er Log(y) positiv. y placeres under 1

Kun positive tal kan placeres på en logaritmisk skala.

Herunder ses en y-akse og 3 søjler med tal.

Søjlen længst til venstre er en sædvanlig tal-skala.

Den midterste tal-skala er den tilsvarende logaritme-skala.

Den 3. tal-skala er magen til den midterste. Tallene er blot skrevet på en anden måde.

Bemærk fx:

Log(1000) = 3 og 1000 er placeret i afstanden 3 over 1 på den logaritmiske skala.

Log(0,01) = -2 og 0,01 er placeret i afstanden -2 over 1 på den logaritmiske skala,
og -2 over betyder 2 under.

På en logaritmisk skala kaldes afstanden mellem hver af ovenstående markeringer en dekade.

Læs her hvorfor grafen for en eksponentiel funktion er lineær,
dvs. en linje eller en del af en linje.

Når vi skal tegne en eksponentiel funktion, skal vi finde tilsvarende x- og y-værdier, hvor y = b· a^x

Der gælder:

Log y = Log ( b· a^x ) = Log b + Log ( a^x ) = Log b + x· Log a

Heraf ses, Log y er en lineær funktion af x.

Hvis grafpunkterne (x, y) derfor afsættes i afstanden Log y fra 1, bliver grafen en ret linje med hældningen Log a

Og det er netop hvad vi gør når vi bruger enkeltlogaritmisk papir

Derfor gælder, at alle eksponentielle funktioner har en lineær graf i et enkelt logaritmisk koordinatsystem.

Der gælder endvidere, at ingen andre funktioner har en lineær graf.

Dette beviser vi dog ikke.

Man kan således ved at tegne en funktion i et enkeltlogaritmisk koordinatsystem afgøre, om funktionen er eksponentiel.

Fordoblings- og halveringskonstant

Ved eksponentielt voksende funktioner tales også om en fordoblingskonstant (fordoblingstid) T₂. Det er den forøgelse i x, der giver anledning til en fordobling af funktionsværdien y.

Tilsvarende tales om en halveringskonstant (halveringstid) T_½ ved eksponentielt aftagende funktioner.

Fordoblings og halveringskonstanterne kan ofte aflæses direkte af grafen ved at finde den x-tilvækst, der giver anledning til en fordobling/halvering.

Der gælder følgende formler:

T₂ =

og T_½ =

I eksempel 3 i lektion 14a beregnede vi a til 0,8766…

Ved hjælp af formlen T_½ = kan vi nu beregne halveringskonstanten for den pågældende eksponentielle funktion.

T_½= Log (0,5) / Log(0,8766…) = 5,2610… = 5,261

Hvis du kender fremskrivningsfaktoren a, kan du beregne T₂eller T_½

Hvis du ikke kender a, men kender 2 støttepunkter, kan du beregne a og derefter T₂eller T_½.

Hvis du kun har en graf, så finder du T₂eller T_½ ved først at finde 2 punkter, der svarer til en fordobling eller halvering i funktionsværdi, og så trække x-værdierne fra hinanden.

Bevis for formlen T₂= forløber således.

Lad x betegne fordoblingskonstanten for en eksponentiel funktion

Der må så gælde:

2b = ba^x

2 = a^x

Log 2 = Log a^x

Log 2 = x·Log a

= x

Altså fordoblingskonstanten er:

Formlen for halveringskonstanten bevises på tilsvarende måde.

2) Se video: LogaritmiskSkala

3) Løs interaktive opgaver: eksponentiel funktion

4) Løs E-opgaver: E-opg_14b_lin_og_exp.htm

5) Løs fra 2006-opgavehæftet 1.014, 1.015 Facitliste

Benyt RegneRobot med link til opgavehæftet.

Link til RegneRobot & opgavehæfte

Link: Indholdsfortegnelse

Lektion 2: Ligninger

Lektion 3: Eksponent og rod

Rod

Lektion 4: Regnearternes hierarki og parentes mm.

Lektion 5: Procent og rente

Lektion 6: Lommeregner , RegneRobot m.m.

Der er ingen opgaver fra 2006-opgavehæftet i denne lektion Lektion 7: Procent og rente fortsat, gennemsnitlig %-vis ændring

Rentefoden / vækstraten r

Antal terminer n

Lektion 8: Indeks

Lektion 9a: Geometri, vinkler, areal af trekant og ensvinklede trekanter

Lektion 9b: Geometri, retvinklede trekanter, Sinus, Cosinus & Tangens

Lektion 9c: Geometri, retvinklede trekanter, Pythagoras’ sætning

Lektion 9d: Geometri, vilkårlige trekanter

Lektion 9e: Geometri, Sinus, Cosinus og Tangens i regneark

Lektion 10a: Sammenhæng mellem variable

Rapportopgave ”Temperatur”

Lektion 10b: Sammenhæng mellem variable

”Ligefrem proportional” eller blot ”proportional”

Lektion 11: Lineære funktioner

Lektion 12: Tegn grafer med pc

Sådan tegnes grafer med pc

Tegn grafer online med, GraphSketch.com som er gratis.

Lektion 13: Logaritmer

Lektion 14a: Eksponentielle funktioner

Lektion 14b: Eksponentielle funktioner

Der er ingen opgaver fra 2006-opgavehæftet i denne lektion
Lektion 7:
Procent og rente fortsat, gennemsnitlig %-vis ændring

Lektion 9a: Geometri, vinkler, areal af trekant og
ensvinklede trekanter